<< Click to Display Table of Contents >> Navigation:  Help Content > Polarimetry and PolInSAR Module > Reference Guide Polarimetry > Polarimetry and PolInSAR - Polarimetry - Pauli Decomposition

Purpose

 

The Pauli coherent decomposition provides an interpretation of a full polarimetric Single Look Complex data set in terms of elementary scattering mechanisms: sphere/plate/trihedral (single- or odd-bounce scattering), dihedral oriented at 0° (double- or even-bounce) and diplane oriented at 45° (qualitatively related also to volume scattering). In general the coherent decomposition approach is suitable for discriminating the scattering of elementary objects (e.g. man made structures).

 

The results are in Slant Range geometry, therefore each of the output RGB channels shall be geocoded in order to be properly displayed in a cartographic system, afterward a new colour composite of the three geocoded RGB channels will be performed.

 

Technical Note

The objective of the coherent decomposition is to express the measured scattering matrix S as the combination of the scattering responses of elementary objects.

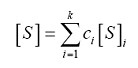
The symbol Si stands for the response of every one elementary objects, whereas ci indicates the weight of Si in the combination leading to the measured S.

 

It has to be pointed out that the scattering matrix S can characterise the scattering processes produced by a given object, and therefore the object itself. This is possible only in those cases where both, the incident and the scattered waves are completely polarized. Consequently, coherent target decompositions can be only employed to study the coherent targets. These scatterers are known as point or pure targets.

 

In a real situation, the measured scattering matrix S corresponds to a complex coherent target. Therefore a direct analysis of the scattering matrix, with the objective to infer the physical properties of the scatterers under study, is often very difficult. Thus the physical properties of the scatterers are extracted and interpreted through the analysis of elementary responses Si  and corresponding coefficients ci .  

 

The decomposition as exposed in not unique in the sense that it is possible to find number of infinite sets Si  in which the scattering matrix S can be decomposed. Nevertheless, only some of the sets Si are convenient to interpret the information content of S.  Three methods are typically employed to characterize coherent scatterers based on the scattering matrix S :

 

•The Pauli Decomposition

•The Krogager Decomposition

•The Cameron Decomposition

 

This functionality provides the decomposition results coming from the Pauli method. Three single channels and their color composite (namely _k2_slc, _k3_slc and _k1_slc respectively assigned to the Red, Green and Blue colors), are generated. The meaning, in terms of scattering mechanism, is as follows:

 

•Even-bounce (HH-VV)

•Dihedral rotated 45 degree (HV+VH)

•Odd-bounce (HH+VV)

 

Input Files

 

Input HH File

Input file names of the scattering matrix (_slc). This file is mandatory.

 

Input HV File

Input file names of the scattering matrix (_slc). This file is mandatory.

 

Input VH File

Input file names of the scattering matrix (_slc). This file is mandatory.

 

Input VV File

Input file names of the scattering matrix (_slc). This file is mandatory.

 

Output Files

 

Output root name

Root file name. This file is mandatory.

 

_pauli_K1_slc

HH + VV polarization combination with the associated header files (.sml, .hdr).

 

_pauli_K2_slc

HH - VV polarization combination with the associated header files (.sml, .hdr).

 

_pauli_K3_slc

HV + VH polarization combination with the associated header files (.sml, .hdr).

 

_pauli_rgb.tif

Color composite using K2, K3, K1 respectively in Red, Green and Blue with the corresponding header file (.sml).

 

Details specific to the Units of Measure and Nomenclature of the output products can be found in the Data Format section.

 

General Functions

 

Exec

The processing step is executed.

 

Store Batch        

The processing step is stored in the batch list. The Batch Browser button allows to load the batch processing list.

 

Close        

The window will be closed.

 

Help

Specific help document section.

 

 

Specific Function(s)

 

None.

 

See Also

 

Task, SARscapeBatch object, SARscapeBatch script example

 

References

 

ESA, Polarimetric SAR Interferometry tutorial

 

Cloude, S.R. and E. Pottier: "A review of target decomposition theorems in radar polarimetry". IEEE Trans. GRS, vol. 34(2), pp. 498-518, Mar. 1996.

 

Cloude, S.R. and E. Pottier: "Symmetry, zero correlations and target decomposition theorems". in Proc. 3rd Int. Workshop on Radar Polarimetry (JIPR ’95), IRESTE, University of Nantes, Mar. 1995, pp. 58–68.