|
<< Click to Display Table of Contents >> Polarimetry and PolInSAR - Polarimetry - Dual Polarimetric Entropy Alpha Anisotropy Decomposition |
  
|
|
<< Click to Display Table of Contents >> Polarimetry and PolInSAR - Polarimetry - Dual Polarimetric Entropy Alpha Anisotropy Decomposition |
  
|
Purpose
The Entropy / Alpha / Anisotropy decomposition performs an eigen-decomposition of the coherency matrix of a full-polarimetric Single Look Complex data set. In order to facilitate the analysis of the physical information provided by the eigen decomposition of the coherency matrix, three secondary parameters are defined as a function of the eigenvalues and eigenvectors:
•Entropy – it is related to degree of randomness of the scattering process. It can vary from 0 to 1.
•Alpha – it relates to the type of scattering mechanism. It can vary from 0° to 90°.
•Anisotropy – it measures the relative importance of the second and third eigenvalue of the eigen decomposition. It can vary from 0 to 1.
In general the incoherent decomposition approach is suitable for discriminating the scattering of complex targets such as natural features.
Technical Note
The scattering matrix S is only able to characterize, from a polarimetric point of view, coherent scatterers. On the contrary, this matrix can not be employed to characterize distributed targets. This type of scatterers can be only characterized, statistically, due to the presence of speckle noise. Since speckle noise must be reduced, only second order polarimetric representations can be used to analysed distributed scatterers. These second order descriptors are the 3 by 3, Hermitian average covariance (C) and the coherency (T) matrices. These two representations are equivalent.
The complexity of the scattering process makes extremely difficult the physical study of a given scatter through the analysis of C or T. Hence, the objective of the incoherent decompositions is to separate the C or T matrices as the combination of the second order descriptors corresponding to simple objects, presenting an easier physical interpretation. These decomposition theorems can be expressed as:
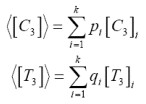
where pi and qi denote the coefficients of the components in C and T .
As in the case of the coherent decomposition, it is desirable that these components present some properties. First at all it is desirable that the components Ci and Ti correspond to pure targets in order to simplify the study. In addition the components should be independent, i.e. orthogonal. The bases in which C orT are not unique. Consequently different incoherent decompositions can be expressed:
•The Freeman Decomposition
•The Huynen Decomposition
•The Eigenvector-Eigenvalue Decomposition
This functionality provides the decomposition results coming from the Eigenvector-Eigenvalue method. The three single channels (i.e. entropy, alpha and anisotropy) and the color channels (i.e. Red, Green, Blue) coming from their linear combination are generated. This combination, which had already been proposed in PolSARPro, consists of:
•Red channel = SQRT(Lambda) * sin(Alpha) * cos(Beta)
•Green channel = SQRT(Lambda) * sin(Alpha) * sin(Beta)
•Blue channel = SQRT(Lambda) * cos(Alpha)
Lambda, Alpha and Beta are defined according to the original Cloude & Pottier paper.
To properly scale the Red, Green and Blue channels for an RGB colour composite we suggest to use the "Tools>Generate Color Composite" functionality.
An important property of this decomposition method is its independency from the orientation of the imaged objects respect to the acquisition sensor (roll-invariance).
Filter Window Type and Window Size
The Entropy / Alpha / Anisotropy decomposition is based on the estimated polarimetric coherency matrix (each polarisation against another one); the window type and size correspond respectively to the method (i.e. "Boxcar" or "Adaptive") and window dimension, which are adopted for the coherence estimate (refer to the relevant technical notes for additional details). The moving window within which the entropy, alpha, and anisotropy values are calculated, it can either be constant and rectangular (Boxcar), or it can vary following the backscatter behaviour (Adaptive).
Input Files
Input HH File
Input file names of the scattering matrix (_slc). This file is mandatory.
Input HV File
Input file names of the scattering matrix (_slc). This file is mandatory.
Input VH File
Input file names of the scattering matrix (_slc). This file is mandatory.
Input VV File
Input file names of the scattering matrix (_slc). This file is mandatory.
Parameters - Principal Parameters
Azimuth Window Size
Window size (in pixel) in azimuth direction. This shall be set proportionally to the multilooking factor.
Range Window Size
Window size (in pixel) in range direction. This shall be set proportionally to the multilooking factor.
Window Type
One of the following options must selected:
Boxcar
A window of constant shape and size is used.
Adaptive
An adaptive process is used to locally estimate the optimal size and shape of the window; this dimension will never exceed the specified window size (in azimuth and range). The adaptive process is based on the local stationary behaviour of the backscattered signal in the different polarizations.
Azimuth Multilook
Number of looks in azimuth.
Range multilook
Number of looks in range.
Grid Size for Suggested Looks
The grid size, in meters, used to tune range and azimuth looks. If the other parameters are manually set, the grid size will not imply a change in their values.
Parameters - Global
It brings to the general section of the Preferences parameters. Any modified value will be used and stored for further processing sessions.
Parameters - Other Parameters
It brings to the general section of the Preferences parameters. Any modified value will be used and stored for further processing sessions.
Output Files
Output root name
Root file name. This file is mandatory.
_alpha
Alpha decomposition parameter and associated header files (.sml, .hdr).
_anisotropy
Anisotropy decomposition parameter and associated header files (.sml, .hdr).
_entropy
Entropy decomposition parameter and associated header files (.sml, .hdr).
.list
List of the decomposition parameters. It is needed for the further Entropy Alpha Anisotropy classification.
_red
Linear combination of the decomposition parameters to use as Red channel for an RGB composite, and associated header files (.sml, .hdr).
_green
Linear combination of the decomposition parameters to use as Green channel for an RGB composite, and associated header files (.sml, .hdr).
_blue
Linear combination of the decomposition parameters to use as Green channel for an RGB composite, and associated header files (.sml, .hdr).
Details specific to the Units of Measure and Nomenclature of the output products can be found in the Data Format section.
General Functions
Exec
The processing step is executed.
Store Batch
The processing step is stored in the batch list. The Batch Browser button allows to load the batch processing list.
Close
The window will be closed.
Help
Specific help document section.
Specific Function(s)
| Looks |
The most appropriate range and azimuth multi-looking factors are calculated. This calculation is performed by taking into account the Cartographic Grid Size, which is set in the relevant SARscape Default Values panel.
Task, SARscapeBatch object, SARscapeBatch script example
References ESA, Polarimetric SAR Interferometry tutorial Cloude, S.R. and E. Pottier: "A review of target decomposition theorems in radar polarimetry". IEEE Trans. GRS, vol. 34(2), pp. 498-518, Mar. 1996. Cloude, S.R. and E. Pottier: "Symmetry, zero correlations and target decomposition theorems". Proc. 3rd Int. Workshop on Radar Polarimetry (JIPR ’95), IRESTE, University of Nantes, Mar. 1995, pp. 58–68. S. R. Cloude: "An entropy based classification scheme for polarimetric SAR data". Proc. IGARSS’95, Florence, Italy, July 1995, pp. 2000–2002.