Help Content > Interferometry Module > Phase Processing - Interferometry Single Steps > 2

Purpose

The filtering of the flattened interferogram enables to generate an output product with reduced phase noise. The Interferometric Coherence (which is an indicator of the phase quality) and the Reference Intensity filtered image, are also generated.

Technical Note

It is possible to select on of the following three filtering methods:

Adaptive

The coherence values are used to set the filter window size; the mean Intensity difference among adjacent pixels is used to identify a stationary area, which defines the maximum dimension (in any case not bigger than the input parameter setting) and the shape of the filtering windows. The process is aimed at preserving even the smallest interferometric fringe patterns.

This filtering procedure is quite expensive in terms of computing time as well as for what concerns the identification of the threshold value to use as Similarity Mean Factor (similarity between the backscatter values measured in the Reference and Secondary Intensity data). On the basis of this factor the areas of the image where the signal intensity is considered stationary are identified. The selection of the pixels to include within each "stationary area", is based on the value of the difference between the mean of the pixels in that area (Mall) and the value of the new pixel (Mnew), which is potentially candidate (this difference is normalized for Mall). The new candidate pixels are identified using a region growing approach.

The formula of the Similarity Mean Factor, which is represented by a digital number in linear scale, can be written as:

(Mall - Mnew) / Mall

It must be noted that several process iterations are typically required in order to set the optimal Similarity Mean Factor. This threshold value can be set from the Preferences>Adaptive Filter>Adaptive Interferogram Filtering>Similarity Mean Factor.

Boxcar

The local fringe frequency is used in order to optimize the band pass filter. The process is aimed at preserving even the smallest interferometric fringe patterns. The processing parameters, which are not directly visible in this processing interface, can be accessed and modified from the Preferences>Adaptive Filter>Boxcar Interferogram Filtering.

Goldstein

The variable bandwidth of the filter, derived directly from the power spectrum of the fringes, smoothes in a selective way the noise frequencies and the signal frequencies. In order to optimize the filter performance the "alpha" parameter, which characterizes the strength of the filter, is handled in an adaptive way on the basis of the local scene coherence: the lower the coherence the stronger the filter.

Several processing parameters, which are not directly visible in this processing interface, can be accessed and modified from the Preferences>Adaptive Filter>Goldstein Interferogram Filtering.

This filtering approach, which is an extension of the Goldstein method, significantly improves fringe visibility and reduces the noise introduced by temporal or baseline related decorrelation. In this implementation the alpha parameter is depending on the coherence: incoherent areas are filtered more than coherent zones. This implies a signal loss minimization, while strongly reducing the level of noise. The use of the coherence generated from the filtered interferogram (option enabled by setting the flag "Coherence from Fint"), must be carefully considered since the phase smoothing, which is produced by the filter itself, causes an over estimation of the coherence (the stronger the filter the higher the coherence values). If the objective is either not to unwrap areas which appear coherent but are actually very noisy or to use of the coherence data for other purposes (i.e. land cover classification or other qualitative/quantitative applications), the coherence shall be generated from the unfiltered interferogram or using the boxcar filtering approach.

Adaptive Non Local InSAR

In order to precisely estimate the coherence and filtering interferograms, a non-local filter, specifically designed for InSAR and based on interferometric phase and amplitude similarity, has been developed. This tool is based on the papers reported in the References paragraph with the addition of a custom locally adaptive similarity probability kernel. This kernel is used to overcome local distortions caused by strong backscattering variations (the so called “rare patches”), typical of the original filter design.

This algorithm implementation considers systematic phase ramp inside the similarity windows (estimated via FFT and removed before the process) to improve the similarity estimation itself and provide a better estimation of the underlying uncoherent phase noise. Moreover, this algorithm overcome the extra smoothing over strong amplitude variations areas between Reference and Secondary acquisitions, typical of the original implementation, exploiting an innovative Central Pixel Modulation based on the previous coherence estimated value.

The number of iterations for the weighted denoising is set to 3 by default.

Non-local-based filtering is an intrinsically, computationally demanding feature, due to its many comparisons between different image areas. Therefore, this tool put the underlying hardware components under stress and requires a significant amount of time. For this reason, our implementation is entirely written in OpenCL to take advantage of the massive level of parallelization offered by modern graphical processing units. Hence, we warmly recommended to use this filter only in combination with a powerful GPU selected as the current OpenCL platform/device under the SARscape Common Preferences. It is always possible to select and rely to a CPU-only OpenCL platform/device, but in such a case performance will roughly be one order of magnitude lower than using a modern GPU.

The results of this tool are the following products:

-Filtered interferogram

-Coherence

-Reference filtered power

-Secondary filtered power

The strength points of this filter with respect to the other filters are the following:

-details preservation in the filtered interferogram, in the coherence and in the power layers, vs homogeneous area stronger filtering

-unbiased coherence estimation (evident mostly in low coherent areas) due to the large processing window size.

-spatial resolution preservation for all the output layers (coherence included) with respect to input resolution; moreover, the spatial resolution is the same for all the derived products differently from the other coherence estimators.

-The coherence is estimated directly from the input differential interferograms and not from the filtered one. For this reason, the coherence can be used for quantitative measurements for land use monitoring.

Coherence generation

The interferometric correlation or Coherence (γ) is the ratio between coherent and incoherent summations:

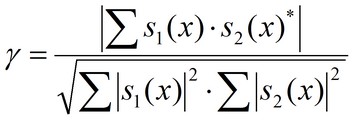
The estimated coherence - which ranges between 0 and 1 - is function of:

-	Systemic spatial de-correlation (i.e. the additive noise).

-	Temporal de-correlation between Reference and Secondary acquisitions.

When working with single look data (i.e. azimuth and range multilooking factors are both set to 1), it could make sense to increase the "Coherence Window Size" (in azimuth and range) in order to increase the number of samples and eventually avoid coherence overestimate problems.

The coherence product has essentially a twofold purpose:

-To determine the quality of the measurement (i.e. interferometric phase). As a rule of thumb, InSAR pairs with low coherence should not be used to derive reliable phase related measurements.

-To extract thematic information relevant to the ground features properties and their temporal changes. This information is enhanced when coupled with the backscattering coefficient (σo) of the Reference and Secondary Intensity data.

As a general rule it can be assumed that the coherence decreases with increasing Reference-Secondary acquisition time distance.

The coherence image can be generated from the input unfiltered interferogram or from the filtered one (refer to the "Input Parameters>Coherence from Fint").

Input Files

Interferogram file

File name of the flattened interferogram (_dint). This file is mandatory.

Input Reference file

File name of the multi-looked Reference Intensity data (_pwr). This file is mandatory.

Input Secondary file

File name of the multi-looked coregistered Secondary Intensity data (_pwr). This file is mandatory.

Parameters - Principal Parameters

Coherence Generation

By setting this flag, the coherence is generated.

Adaptive Filter

By setting this flag, the input interferogram is filtered. This flag is disabled when the "Local Frequency Removal (Range and Azimuth)" is set to a value higher than zero; indeed in this case the _fint file should have already been generated.

Filtering method

The choice is given between the following filtering methods according to the default values of the filtering section of the Preferences parameters:

•Adaptive window;

•Boxcar window;

•Goldstein.

Refer to the Preferences description for further information about these methods.

Coherence from Fint

By setting this flag, the coherence is computed using the filtered interferogram (_fint) instead of the unfiltered one (_dint).

Parameters - Global

It brings to the general section of the Preferences parameters. Any modified value will be used and stored for further processing sessions.

Parameters - Filtering

It brings to the filtering section of the Preferences parameters. Any modified value will be used and stored for further processing sessions.

Parameters - Other Parameters

It brings to the general section of the Preferences parameters. Any modified value will be used and stored for further processing sessions.

Output Files

Output Root Name

Name of the output root. This file is mandatory.

_fint

Filtered interferogram with the associated header files (.sml, .hdr). This file is generated only if the Adaptive Filter flag is selected.

_fint_ql.tiff and/or _fint_qlt.tiff

Tiff image of the filtered interferogram. The creation of these files depends on the selection of "quick look format" in the parameters. It uses a cyclic color scale ranging from -pi to +pi which is reported here below:

_pwr_fil

Filtered Intensity - from Reference and Secondary combination - with the associated header files (.sml, .hdr). This file is generated only if the "Adaptive" filter is selected.

_cc

Estimated coherence with the associated header files (.sml, .hdr). This file is generated only if the Coherence Generation flag is selected.

Details specific to the Units of Measure and Nomenclature of the output products can be found in the Data Format section.

General Functions

Exec

The processing step is executed.

Store Batch

The processing step is stored in the batch list. The Batch Browser button allows to load the batch processing list.

The window will be closed.

Help

Specific help document section.

Specific Function(s)

None.

Interferometry - Phase processing - 2 - Adaptive Filter and Coherence Generation

Interferometry - Phase processing - 2 - Adaptive Filter and Coherence Generation