LADFIT

The LADFIT function fits the paired data {xi, yi} to the linear model, y = A + Bx, using a “robust” least absolute deviation method.

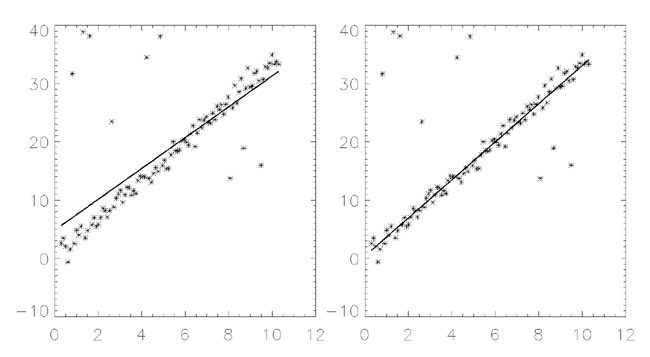
The figure below displays a two-dimensional distribution that is fitted to the model y = A + Bx, using a minimized Chi-square error criterion (left) and a “robust” least absolute deviation technique (right). The use of the Chi-square error statistic can result in a poor fit due to an undesired sensitivity to outlying data.

This routine is written in the IDL language. Its source code can be found in the file ladfit.pro in the lib subdirectory of the IDL distribution.

Example

; Define two n-element vectors of paired data:

X = [-3.20, 4.49, -1.66, 0.64, -2.43, -0.89, -0.12, 1.41, $

   2.95, 2.18, 3.72, 5.26]

Y = [-7.14, -1.30, -4.26, -1.90, -6.19, -3.98, -2.87, -1.66, $

   -0.78, -2.61, 0.31, 1.74]

; Sort the X values into ascending order, and sort the Y values to

; match the new order of the elements in X:

XX = X[SORT(X)]

YY = Y[SORT(X)]

; Compute the model parameters, A and B:

PRINT, LADFIT(XX, YY)

IDL prints:

-3.15301 0.930440

Syntax

Result = LADFIT( X, Y [, ABSDEV=variable] [, /DOUBLE] )

Return Value

The result is a two-element vector containing the model parameters, A and B.

Arguments

X

An n-element vector containing the independent variable values. X may be of type integer, floating point, or double-precision floating-point. Note that the X vector must be sorted into ascending order.

Y

An n-element integer, single-, or double-precision floating-point vector. Note that the elements of the Y vector must be paired with the appropriate elements of X.

Keywords

ABSDEV

Set this keyword to a named variable that will contain the mean of the absolute deviation of the Result and Y.

DOUBLE

Set this keyword to force the computation to be done in double-precision arithmetic.

Version History

4.0	Introduced

See Also

COMFIT, CURVEFIT, LINFIT, SORT