IMSL_NONLINREGRESS

The IMSL_NONLINREGRESS function fits a nonlinear regression model.

This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.

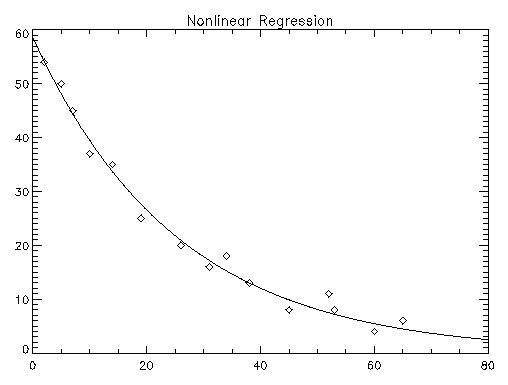
The IMSL_NONLINREGRESS function fits a nonlinear regression model using least squares. The nonlinear regression model is

y_i = f(x_i;θ) + ε_i      i = 1, 2, ..., n

where the observed values of the y_i’s constitute the responses or values of the dependent variable, the known x_i’s are the vectors of the values of the independent (explanatory) variables, θ is the vector of p regression parameters, and the ε_i’s are independently distributed normal errors with mean zero and variance σ². For this model, a least-squares estimate of θ is also a maximum likelihood estimate of θ.

The residuals for the model are as follows:

e_i(θ) = y_i – f(x_i; θ)     i = 1, 2, ..., n

A value of θ that minimizes:

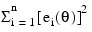
is a least-squares estimate of θ. IMSL_NONLINREGRESS is designed so that the values of the function f(xi ; θ) are computed one at a time by a user-supplied function.

The IMSL_NONLINREGRESS function is based on MINPACK routines LMDIF and LMDER by Moré et al. (1980) that use a modified Levenberg-Marquardt method to generate a sequence of approximations to a minimum point. Let:

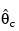
be the current estimate of θ. A new estimate is given by:

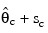
where sc is a solution to the following:

Here:

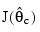
is the Jacobian evaluated at:

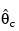
The algorithm uses a “trust region” approach with a step bound of δ_c. A solution is first obtained for µ_c = 0. If:

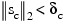
this update is accepted; otherwise, µ_c is set to a positive value and another solution is obtained. The method is discussed by Levenberg (1944), Marquardt (1963), and Dennis and Schnabel (1983, pp. 129 –147, 218 –338).

If a user-supplied function is specified in Jacobian, the Jacobian is computed analytically; otherwise, forward finite differences are used to estimate the Jacobian numerically. In the latter case, especially if single precision is used, the estimate of the Jacobian may be so poor that the algorithm terminates at a noncritical point. In such instances, you should either supply a Jacobian function, use the Double keyword, or do both.

Programming Notes

Nonlinear regression allows substantial flexibility over linear regression because you can specify the functional form of the model. This added flexibility can cause unexpected convergence problems for users who are unaware of the limitations of the software. Also, in many cases, there are possible remedies that may not be immediately obvious. The following is a list of possible convergence problems and some remedies. There is no one-to-one correspondence between the problems and the remedies. Remedies for some problems also may be relevant for other problems.

• A local minimum is found. Try a different starting value. Good starting values often can be obtained by fitting simpler models. For example, for a nonlinear function:

  

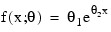
• Good starting values can be obtained from the estimated linear regression coefficients:

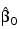  and

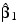
• From a simple linear regression of ln y on x. The starting values for the nonlinear regression in this case would be:

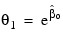  and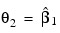

• If an approximate linear model is not clear, then simplify the model by reducing the number of nonlinear regression parameters. For example, some nonlinear parameters for which good starting values are known could be set to these values in order to simplify the model for computing starting values for the remaining parameters.
• The estimate of θ is incorrectly returned as the same or very close to the initial estimate. This occurs often because of poor scaling of the problem, which might result in the residual sum of squares being either very large or very small relative to the precision of the computer. The keywords allow control of the scaling.
• The model is discontinuous as a function of θ. (The function f(x;θ) can be a discontinuous function of x.)
• Overflow occurs during the computations. Make sure the supplied functions do not overflow at some value of θ.
• The estimate of θ is going to infinity. A parameterization of the problem in terms of reciprocals may help.
• Some components of θ are outside known bounds. This can sometimes be handled by making a function that produces artificially large residuals outside of the bounds (even though this introduces a discontinuity in the model function).

Examples

Example 1

In this example (Draper and Smith 1981, p. 518), the following nonlinear model is fit:

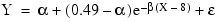
.RUN

FUNCTION fcn, x, theta

RETURN, theta(0) + (0.49 - theta(0)) $

*EXP(theta(1)*(x(0) - 8))

END

 

x = [10, 20, 30, 40]

y = [0.48, 0.42, 0.40, 0.39]

n_parameters = 2

theta_hat = IMSL_NONLINREGRESS('fcn', n_parameters, x, y)

PRINT, 'Estimated Coefficients:', theta_hat

Example 2

Consider the nonlinear regression model and data set discussed by Neter et al. (1983, pp. 475–478):

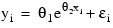
There are two parameters and one independent variable. The data set considered consists of 15 observations. The results are shown in the figure that follows.

.RUN

FUNCTION fcn, x, theta

; Define function that defines nonlinear regression problem.

RETURN, theta(0) * EXP(x(0) * theta(1))

END

 

.RUN

FUNCTION jac, x, theta

; Define the Jacobian function. fjac = theta

; The following assignment produces array of correct size to

; use as the return value of the Jacobian.

fjac[0] = exp(theta[1] * x[0])

fjac[1] = theta[0] * x[0] * EXP(theta[1] * x[0])

RETURN, fjac

; Compute the Jacobian.

END

 

.RUN

PRO nlnreg_ex

; Define x and y.

x = [2, 5, 7, 10, 14, 19, 26, 31, 34, 38, 45, 52, 53, 60, 65]

y = [54, 50, 45, 37, 35, 25, 20, 16, 18, 13, 8, 11, 8, 4, 6]

theta_hat = IMSL_NONLINREGRESS('fcn', 2, x, y, $

Theta_Guess = [60, -0.03], $

Grad_Eps = 0.001, Jacobian = 'jac')

PLOT, x, y, Psym = 4, Title = 'Nonlinear Regression'

; Plot original data.

xtmp = 80 * FINDGEN(200)/199

OPLOT, xtmp, theta_hat(0) * EXP(xtmp * theta_hat(1))

; Plot regression.

END

Errors

Informational Errors

STAT_STEP_TOLERANCE: Scaled step tolerance satisfied. The current point may be an approximate local solution, but it is also possible that the algorithm is making very slow progress and is not near a solution or that Step_Eps is too big.

Warning Errors

STAT_LITTLE_FCN_CHANGE: Both actual and predicted relative reductions in the function are less than or equal to the relative function tolerance.

STAT_TOO_MANY_ITN: Maximum number of iterations exceeded.

STAT_TOO_MANY_FCN_EVAL: Maximum number of function evaluations exceeded.

STAT_TOO_MANY_JACOBIAN_EVAL: Maximum number of Jacobian evaluations exceeded.

STAT_UNBOUNDED: Five consecutive steps have been taken with the maximum step length.

STAT_FALSE_CONVERGENCE: Iterates appear to be converging to noncritical point.

Syntax

Result = IMSL_NONLINREGRESS(Fcn, N_Parameters, X, Y [, ABS_EPS_SSE=value] [, DF=variable] [, /DOUBLE] [, JACOBIAN=string] [, GRAD_EPS=value] [, ITMAX=value] [, MAX_JAC_EVALS=value] [, MAX_SSE_EVALS=value] [, MAX_STEP=value] [, N_DIGIT=value] [, PREDICTED=variable] [, R_MATRIX=variable] [, R_RANK=variable] [, REL_EPS_SSE=value] [, RESIDUAL=variable] [, STEP_EPS=value] [, SSE=variable] [, THETA_GUESS=array] [, THETA_SCALE=array] [, TOLERANCE=value] [, TRUST_REGION=value])

Return Value

One-dimensional array of length N_Parameters containing solution: θˆ for the nonlinear regression coefficients.

Arguments

Fcn

Scalar string specifying the name of a user-supplied function to evaluate the function that defines the nonlinear regression problem. Function fcn accepts the following input parameters and returns a scalar float:

• x: One-dimensional array containing the point at which point the function is evaluated.
• theta: One-dimensional array containing the current values of the regression coefficients. Function fcn returns a predicted value at the point x. In the following, f(xi; θ), or just fi, denotes the value of this function at the point xi, for a given value of θ. (Both xi and θ are arrays.)

N_Parameters

Number of parameters to be estimated.

X

Two-dimensional array containing the matrix of independent (explanatory) variables.

Y

One-dimensional array of length N_ELEMENTS (x(*, 0)) containing the dependent (response) variable.

Keywords

ABS_EPS_SSE (optional)

Absolute SSE function tolerance. Default: max(10 –20, ε2), max(10 – 40, ε2) in double, where ε is the machine precision

DF (optional)

Named variable into which the degrees of freedom is stored.

DOUBLE (optional)

If present and nonzero, double precision is used.

JACOBIAN (optional)

Scalar string specifying the name of a user-supplied function to compute the i-th row of the Jacobian. This keyword accepts the following parameters:

• X: One-dimensional array of length N_ELEMENTS (x(0, *)) containing the data values corresponding to the i-th row.
• Theta: One-dimensional array of length N_Parameters containing the regression coefficients for which the Jacobian is evaluated. The return value of this function is an array of length N_Parameters containing the computed N_Parameters row of the Jacobian for observation i at Theta. Note that each derivative ∂f(xi)/¹∂θj should be returned in element (j – 1) of the returned array for j = 1, 2, ..., n parameters.

GRAD_EPS (optional)

Scaled gradient tolerance. The j-th component of the scaled gradient at θ is calculated as:

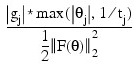
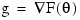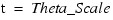where and and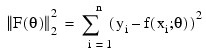

The value F(θ) is the vector of the residuals at the point θ. Default: 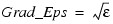in double), where ε is the machine precision.

ITMAX

Maximum number of iterations. Default: 100

MAX_JAC_EVALS (optional)

Maximum number of Jacobian evaluations. Default: 400

MAX_SSE_EVALS (optional)

Maximum number of SSE function evaluations. Default: 400

MAX_STEP (optional)

Maximum allowable step size. Default: 1000 max(ε₁, ε₂), where ε₁ = (t^Tθ₀)^1/2, ε₂ = ||t||₂  , t = THETA_SCALE, and θ₀ = THETA_GUESS.

N_DIGIT (optional)

Number of good digits in the function. Default: machine dependent

PREDICTED

Named variable into which the one-dimensional array, containing the predicted values at the approximate solution, is stored.

R_MATRIX (optional)

Named variable into which the two-dimensional array of size N_Parameters x N_Parameters, containing the R matrix from a QR decomposition of the Jacobian, is stored.

R_RANK (optional)

Named variable into which the rank of the R matrix is stored. A rank of less than N_Parameters may indicate the model is overparameterized.

RESIDUAL (optional)

Named variable into which the one-dimensional array, containing the residuals at the approximate solution, is stored.

STEP_EPS (optional)

Scaled step tolerance. The j-th component of the scaled step from points θ and θ′ is computed as:

θ – θ′

--------------j-----------j---------- max( θj , 1 ⁄ tj )

where t = THETA_SCALE. Default: ε2/ 3, where ε is machine precision

SSE

Named variable into which the residual sum of squares is stored.

REL_EPS_SSE (optional)

Relative SSE function tolerance. Default: Rel_Eps_Sse = max(10–10, ε2 / 3), max (10– 20, ε2 / 3) in double, where ε is the machine precision

THETA_GUESS (optional)

Array with N_Parameters components containing an initial guess. Default: THETA_GUESS(*) = 0

THETA_SCALE (optional)

One-dimensional array of length N_Parameters containing the scaling array for θ. Keyword THETA_SCALE is used mainly in scaling the gradient and the distance between two points. See keywords Grad_Eps and Step_Eps for more details. Default: Theta_Scale(*) = 1

TOLERANCE (optional)

False convergence tolerance. Default: 100 * ε, where ε is machine precision.

TRUST_REGION (optional)

Size of initial trust region radius. The default is based on the initial scaled Cauchy step.

Version History

6.4	Introduced

See Also

IMSL_NONLINOPT