IMSL_KELVIN_KEI0
The IMSL_KELVIN_KEI0 function evaluates the Kelvin function of the second kind, kei, of order zero.
This routine requires an IDL Advanced Math and Stats license. For more information, contact your sales or technical support representative.
The modified Kelvin function kei0(x) is defined to be 
. The Bessel function K0(x) is defined as:
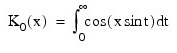
If the keyword DERIVATIVE is set, the function kei0′(x) is defined to be:
The IMSL_KELVIN_KEI0 function is based on the work of Burgoyne (1963). If x < 0, NaN (Not a Number) is returned. If x ≥ 119, zero is returned.
Example
In this example, kei0(0.4) and kei0′(0.6) are evaluated.
PRINT, IMSL_KELVIN_KEI0(0.4)
-0.703800
PRINT, IMSL_KELVIN_KEI0(0.6, /DERIVATIVE)
0.348164
Syntax
Result = IMSL_KELVIN_KEI0(X [, DERIVATIVE=value] [, /DOUBLE])
Return Value
The value of the Kelvin function of the second kind, kei, of order zero evaluated at x.
Arguments
X
Argument for which the function value is desired.
Keywords
DERIVATIVE (optional)
If present and nonzero, then the derivative of the Kelvin function of the second kind, kei, of order zero evaluated at x is computed.
DOUBLE (optional)
If present and nonzero, then double precision is used.
Version History
|
6.4 |
Introduced |