FLAASH® Background

Unlike many other atmospheric correction programs that interpolate radiation transfer properties from a pre-calculated database of modeling results, FLAASH incorporates the MODTRAN radiation transfer code. You can choose any of the standard MODTRAN model atmospheres and aerosol types to represent the scene; a unique MODTRAN solution is computed for each image. ENVI uses MODTRAN version 6.

MODTRAN 6 includes line-by-line capabilities. MODTRAN is a band-model based code, which provides a computational spectral resolution of 0.1 cm -1. This limits the range of application-to-system operating at narrow-to-coarse spectral resolutions, generally greater than 0.2 cm-1 (i.e., includes some filter function averaging). For systems involving active illumination using lasers, much higher spectral resolution is required. MODTRAN 6 has added the Line-By-Line option to provide high resolution radiative transfer calculations and serve as a means of validating the more approximate, but much faster, band model radiative transfer algorithms.

FLAASH also includes the following features:

FLAASH starts from a standard equation for spectral radiance at a sensor pixel, L, that applies to the solar wavelength range (thermal emission is neglected) and flat, Lambertian materials or their equivalents. The equation is as follows:

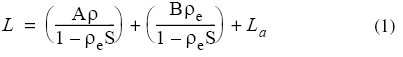
Where:

ρ is the pixel surface reflectance

ρe is an average surface reflectance for the pixel and a surrounding region

S is the spherical albedo of the atmosphere

La is the radiance back scattered by the atmosphere

A and B are coefficients that depend on atmospheric and geometric conditions but not on the surface.

Each of these variables depends on the spectral channel; the wavelength index has been omitted for simplicity. The first term in Equation (1) corresponds to radiance that is reflected from the surface and travels directly into the sensor, while the second term corresponds to radiance from the surface that is scattered by the atmosphere into the sensor. The distinction between ρ and ρe accounts for the adjacency effect (spatial mixing of radiance among nearby pixels) caused by atmospheric scattering. The adjacency effect correction which sets ρe = ρ. More accurate reflectance retrievals result when adjacency correction is enabled; however, there may be occasions when it is desirable to ignore this effect. For example, this correction can result in significant reflectance errors at short wavelengths, especially under hazy conditions and when strong contrasts occur among the materials in the scene.

The values of A, B, S and La are determined from MODTRAN calculations that use the viewing angles, solar angles, mean surface elevation, and assume a certain model atmosphere, aerosol type, and visible range.

The values of A, B, S and La are strongly dependent on the water vapor column amount, which is generally not well known and may vary across the scene. To account for unknown and variable column water vapor, the MODTRAN calculations are looped over a series of different column amounts, then selected wavelength channels of the image are analyzed to retrieve an estimated amount for each pixel. Specifically, radiance averages are gathered for two sets of channels: an absorption set centered at a water band (typically 1130 nm) and a reference set of channels taken from just outside the band. A lookup table for retrieving the water vapor from these radiances is constructed.

Note: For images that do not contain bands in the appropriate wavelength positions to support water retrieval (for example, Landsat or SPOT), the column water vapor amount is determined by the user-selected atmospheric model.

After the water retrieval is performed, Equation (1) is solved for the pixel surface reflectances in all of the sensor channels. The solution method involves computing a spatially averaged radiance image Le, from which the spatially averaged reflectance ρe is estimated using the approximate equation:

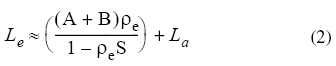
Spatial averaging is performed using a point-spread function that describes the relative contributions to the pixel radiance from points on the ground at different distances from the direct line of sight. For accurate results, cloud-containing pixels must be removed prior to averaging. The cloudy pixels are found using a combination of brightness, band ratio, and water vapor tests, as described by Matthew et al. (2000).

The FLAASH model includes a method for retrieving an estimated aerosol/haze amount from selected dark land pixels in the scene. The method is based on observations by Kaufman et al. (1997) of a nearly fixed ratio between the reflectances for such pixels at 660 nm and 2100 nm. FLAASH retrieves the aerosol amount by iterating Equations (1) and (2) over a series of visible ranges, for example, 17 km to 200 km. For each visible range, it retrieves the scene-average 660 nm and 2100 nm reflectances for the dark pixels, and it interpolates the best estimate of the visible range by matching the ratio to the average ratio of ~0.45 that was observed by Kaufman et al. (1997). Using this visible range estimate, FLAASH performs a second and final MODTRAN calculation loop over water.

References

Adler-Golden, S. M., M. W. Matthew, L. S. Bernstein, R. Y. Levine, A. Berk, S. C. Richtsmeier, P. K. Acharya, G. P. Anderson, G. Felde, J. Gardner, M. Hoke, L. S. Jeong, B. Pukall, A. Ratkowski, and H.-H Burke, 1999. Atmospheric Correction for Short-wave Spectral Imagery Based on MODTRAN4. SPIE Proceedings on Imaging Spectrometry, Vol. 3753, pp. 61-69.

Berk, A., L. S. Bernstein, G. P. Anderson, P. K. Acharya, D. C. Robertson, J.H. Chetwynd, and S. M. Adler-Golden, 1998. MODTRAN Cloud and Multiple Scattering Upgrades with Application to AVIRIS. Remote Sensing of Environment, Vol. 65, pp. 367-375.

Berk A., L. S. Bernstein, and D. C. Robertson, 1989. MODTRAN: a moderate resolution model for LOWTRAN7. GL-TR-89-0122. Air Force Geophysical Laboratory, Hanscom AFB, MA. p. 38.

Kaufman, Y. J., A. E. Wald, L. A. Remer, B.-C. Gao, R.-R. Li, and L. Flynn, 1997. The MODIS 2.1-mm Channel-Correlation with Visible Reflectance for Use in Remote Sensing of Aerosol. IEEE Transactions on Geoscience and Remote Sensing. Vol. 35, pp. 1286-1298.

Matthew, M. W., S. M. Adler-Golden, A. Berk, S. C. Richtsmeier, R. Y. Levine, L. S. Bernstein, P. K. Acharya, G. P. Anderson, G. W. Felde, M. P. Hoke, A. Ratkowski, H.-H. Burke, R. D. Kaiser, and D. P. Miller, 2000. Status of Atmospheric Correction Using a MODTRAN4-based Algorithm. SPIE Proceedings, Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VI. Vol. 4049, pp. 199-207.

Cloud Classes

Some classes in the cloud mask are intermediate values that do not represent clouds. The values are assigned during separate stages of the cloud detection method and are later combined into a mask of cloudy/not cloudy. The following are the classes in the output cloud raster that result from these possible combinations:

The cloud detection algorithms rely on bands that are sensitive to water vapor absorption. If a cirrus band around 1.3 microns is not available, the detection method will not find the classes 'cirrus' and 'thick cirrus'. The classes at and above 'AGL' require at least one sensor band near 1.13 microns, 0.94 microns, or 0.82 microns. The cloud masking routine is disabled if none of those bands are available.

Spectral Polishing

Spectral polishing is a term used by Boardman (1998) for a linear re-normalization method that reduces spectral artifacts in hyperspectral data using only the data itself. The basic assumptions are as follows:

The gains and offsets are generated from the reference pixels by performing a linear fit of the smoothed spectra to the original spectra. Boardman’s original algorithm, which smooths by Legendre polynomial fitting, is available from the Toolbox under Radiometric Correction > EFFORT Polishing.

The FLAASH polishing algorithm yields similar results with less input data. The smoothing is performed with a running average over n adjacent channels (where n is defined as the polishing width). Spectrum endpoint and missing-channel complications are limited if only a modest amount of smoothing is desired (n is low). For example, a polishing width of 2 is useful for removing residual sawtooth noise caused by a dark current offset between odd-numbered and even-numbered channels, as seen in early AVIRIS data. A wider polishing width (for example, 5 to 11) is better for removing larger-scale artifacts such as atmospheric absorption band residuals.

The reference pixels are selected as follows:

  1. For each pixel, a smoothed spectrum is calculated.
  2. The difference between the smoothed spectrum and the unsmoothed spectrum is calculated for each measured wavelength.
  3. The RMS of the smoothed-unsmoothed difference at each wavelength is calculated, and normalized by dividing by the mean reflectance over all wavelengths for the pixel.
  4. The pixels with the lowest ten percent of normalized RMS differences are selected from among the cloud-free, non-blank, and non-vegetated pixels.
  5. The normalized RMS differences for the selected pixels are put into a histogram, and the pixels that fall into the lower half of the histogram are selected to be reference pixels for the calculation of the gain. This eliminates artifacts often found using EFFORT with a vegetated scene.
  6. The gain factor for the linear transformation is computed as the ratio of the RMS smoothed to RMS un-smoothed spectrum for these pixels. There is no offset in the transformation. For this reason, very dark pixels such as water are essentially unaffected by the FLAASH polishing.

Reference

Boardman, J. W. 1998. Leveraging the high dimensionality of AVIRIS data for improved sub-pixel target unmixing and rejection of false positives: mixture tuned matched filtering, In: 7th JPL Airborne Geoscience Workshop, pp. 55-56.

Wavelength Calibration

An accurate wavelength calibration is critical for atmospherically correcting hyperspectral data. Even slight errors in the locations of the band center wavelengths can introduce significant errors into the water retrieval process, and reduce the overall accuracy of the modeled surface reflectance results.

When you run FLAASH, ENVI creates the following files in the FLAASH output directiory:

If you find that the corrected wavelengths are an improvement after FLAASH processing is complete, you may want to apply them to the original input radiance image. To do this:

  1. In the Toolbox, select Raster Management > Edit ENVI Header. The Data Selection dialog appears.

  2. Open the original input radiance file and click OK. The Edit ENVI Header dialog appears.

  3. Select the Spectral tab.

  4. In the Wavelength field, click the Import from ASCII File button, select the spectral_cal.txt file, then click OK.

If you do any further processing of the radiance file in FLAASH after the corrected wavelengths have been applied, set the Sensor Autocalibration value on the Misc. tab to No.

Reference

For algorithm details:

Felde, G. W., G. P. Anderson, S. M. Adler-Golden, M. W. Matthew, and A. Berk, 2003. Analysis of Hyperion Data with the FLAASH Atmospheric Correction Algorithm. Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery IX. SPIE Aerosense Conference, Orlando. 21-25 April 2003.